Nous voici à l'épisode 5 de l'introduction à LaTeX de Fabien Conus, mise à jour (la version originale se trouvant ici). Cette partie traite exclusivement des mathématiques, et n'a été que peu modifiée, ce qui n'est guère étonnant : le traitement des maths par LaTeX étant excellent depuis le début, et faisant référence dans le milieu scientifique, il n'a guère été modifié au fil des années :-)
Bonne lecture !
Franck Pastor
Comme je l'ai écrit en commentaires (hélas aujourd'hui disparus) du test de Renan Fuhrimann sur MathMagic, je considère qu'il est totalement improductif de devoir écrire à la souris. Et pourtant, c'est ce que les éditeurs d'équations vous proposent (que ce soit celui de Word, MathMagic, ou un autre). Je pense pour ma part qu'écrire mes mathématiques sur mon clavier, sans le quitter, est la situation optimale. De plus, LaTeX offre le meilleur rendu d'équations qu'il soit possible d'obtenir (bien sûr, la beauté est toujours subjective). Vous pouvez aller voir un article publié par le service informatique de l'EPFL qui compare entre autres le rendu des équations avec Word, Framemaker et LaTeX.
L'écriture des mathématiques dans LaTeX est très très complète, et il me serait donc bien difficile d'être exhaustif. Je vous en propose donc un tour d'horizon plutôt qu'une visite complète, à l'image des autres articles de cette série.
Les mathématiques peuvent s'écrire soit dans le cours du texte, soit en dehors. Nous commencerons par examiner le premier cas.
Les formules dans le cours du texte
Pour écrire une équation dans le texte, il faut simplement l'encadrer de deux signes $. L'équation est alors traitée dans le mode mathématique de LaTeX. Par exemple :
| Einstein a écrit $E=mc^2$. |
Vous le voyez, l'écriture d'une équation est assez naturelle. La mise en exposant se fait comme en programmation avec le signe « ^ ».
Après compilation, voici ce qu'on obtient :
![]()
Vous aurez noté que les noms de variables sont automatiquement mis en italique dans la formule sortie, ainsi qu'il est de règle dans toute publication mathématique.
Précisons tout de suite qu'en mode mathématique, les espaces entrés au clavier ne sont pas du tout pris en compte. LaTeX prend lui-même complètement en charge les espaces entre symboles. Que vous ayiez entré :
| $E = mc^2$ |
ou
| $E = m c^2$ |
serait revenu exactement au même pour la formule finale. Profitez-en pour « aérer » les codages de vos formules dans votre document LaTeX, ce sera apprécié à la relecture dudit document ;-)
Cependant, LaTeX fournit plusieurs commandes pour insérer en mode mathématique une espace horizontale plus ou moins grande par nous-mêmes. Les plus utiles, vous les connaissez déjà, elles fonctionnent aussi dans une formule : « \, » pour une espace fine, et « \ » (contre-oblique + espace-clavier) pour une espace-mot. Vous ne devriez avoir à les utiliser qu'avec parcimonie : LaTeX se débrouille en général très bien tout seul dans la gestion des espaces entre symboles.
Autre particularité du mode mathématique de LaTeX : les sauts de ligne n'y sont pas admis. Si vous laissez une ligne blanche au milieu du code de votre formule, LaTeX signalera une erreur.
Essayons maintenant une formule plus compliquée :
| Mais Einstein a dit aussi $E= \sqrt{p^2c^2 + m_0^2c^4}$. |
On y voit d'abord la commande \sqrt qui dessine une racine carrée (« square root » en anglais). Puis les mises en exposant, mais aussi une mise en indice qui se fait grâce au caractère « _ ». Voyez le résultat :
![]()
Les mises en indice ou en exposant ne prennent a priori que le premier caractère qui les suit (sauf si c'est une commande). Pour mettre plusieurs caractères en indice ou en exposant, il faut utiliser les accolades. Par exemple, le code
| $2^2+6=256$ |
donnera
![]()
et donc une équation fausse, tandis que
| $2^{2+6}=256$ |
donnera
![]()
ce qu'on voulait obtenir.
Pour écrire une fraction, on utilise la commande \frac :
| $\frac{x}{y} = 2$. |
Les formules hors-texte
Bien entendu, toutes ces opérations peuvent s'emboîter les unes dans les autres, mais cela donne lieu à des équations de taille assez conséquente. Il ne sera donc pas conseillé de les placer dans le texte, mais plutôt sur une nouvelle ligne, et centrées pour bien les mettre en évidence.
Pour cela, nous allons placer l'équation dans un environnement equation (qui l'eût cru ?). Cet environnement fait également entrer LaTeX en mode mathématique, et toutes les règles et commandes que vous avez vues précédemment pour les formules dans le cours du texte s'appliquent aussi ici. Mais l'environnement equation se charge en outre de mettre en valeur la formule, en particulier en la plaçant sur une nouvelle ligne légèrement décalée vers le bas, et en la centrant. Par exemple :
| \begin{equation} \frac{x^{\left(\sqrt{p^2c^2 + m_0^2c^4} - y_0^4 \right)} - 2y + 8}{(y+x)^2} = 4K_1 + 3x. \end{equation} |
donnera
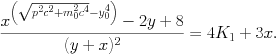
J'attire votre attention sur la qualité de l'équation produite.
Vous aurez noté l'utilisation de « \left( » et de« \right) » . En effet, pour placer des parenthèses, il suffit d'écrire des parenthèses (sans blague ?) Mais si vous entrez ceci :
| 2(\frac{x}{y}) = 8 |
vous obtiendrez ça :
ce qui n'est pas très joli. En utilisant « \left( » et « \right) », LaTeX adapte lui-même la taille des parenthèses au contenu :
ce qui est bien mieux. Bien entendu, ceci s'applique également aux crochets ([ et ]) et aux accolades. Par contre pour ces dernières, leur utilisation « simple » se fera avec les commande \{ et \}. En effet, l'accolade elle-même est réservée par LaTeX pour les arguments des commandes.
Revenons à notre environnement equation. Si vous avez vous-même compilé le code exposé, vous aurez remarqué que l'équation a été automatiquement numérotée, avec le numéro placé en vis-à-vis à droite de l'équation (ce numéro n'a pas été montré ici, l'ensemble équation-numéro cadrant assez mal sur cette page). Vous pouvez donc évidemment lui faire référence. Ceci se passe toujours de la même manière, à savoir utiliser un \label pour l'étiqueter et un \ref pour faire la référence elle-même :
| \begin{equation} 2\left(\frac{x}{y}\right)=8. \label{eq:xy} \end{equation} L'équation~\ref{eq:xy} nous donne la relation entre $x$ et $y$. |
Si vous désirez ne pas numéroter une équation, vous la placerez simplement dans un environnement displaymath, ou plus simplement entre les commandes \[ et \], comme ceci :
| \[ 2\left(\frac{x}{y}\right)=8. \] |
Mais vous ne pourrez alors pas y faire référence.
Signalons au passage une application importante des signes « ^ » et « _ » : indiquer aux opérateurs leurs éventuelles bornes supérieures et inférieures. C'est notamment le cas pour les opérateurs de sommation, d'intégration et de limite.
| \[ \lim_{x \to \infty} \frac{1}{x} = 0 \qquad \sum_{n=1}^{\infty}\frac{1}{n^2} = \frac{\pi^2}{6} \qquad \int_0^1 x \, dx = \frac{1}{2} \] |
Pour cet exemple, nous avons introduit les commandes \int, \sum et \lim (dont le sens est suffisamment transparent) pour les opérateurs, ainsi que les commandes\to, \pi et \infty pour respectivement la flèche à droite, la lettre grecque « pi » et le symbole « infini ». Ce qui ici donnera
Les équations ci-dessus sont restées sur la même ligne, séparées par une espace horizontale produite par la commande \qquad, de longueur égale à deux cadratins (le cadratin est la taille de la police courante, 10, 11 ou 12 pt). Cette nouvelle commande d'espacement est également valable en mode texte, de même que la commande \quad produisant une espace d'un cadratin.
Alignement vertical des équations
Le principal handicap des environnements du type equation ou displaymath est précisément qu'ils ne permettent pas l'écriture sur plusieurs lignes. Pour pallier ceci, LaTeX fournit l'environnement eqnarray. Ce dernier a l'avantage de vous permettre d'aligner vos équations. Il fonctionne en effet comme un tableau (que nous avons vu dans la partie précédente) à trois colonnes avec un alignement rcl :
| \begin{eqnarray} 2\left(\frac{x}{y}\right) &=& 8,\\ \frac{x}{y} &=& \frac{8}{2}\\ &=& 4. \end{eqnarray} |
Vous remarquerez que comme pour un tableau, on utilise l'esperluette & pour aligner les éléments. Dans cet exemple, on s'assure que les trois signes = seront alignés verticalement :
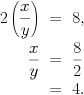
Dans l'environnement eqnarray, chaque ligne est numérotée (je n'ai pas montré non plus les numéros ici). Pour y faire référence, il s'agit de placer un \label à la fin de chaque ligne (avant la commande \\). Si vous ne désirez pas numéroter les équations, il faut utiliser l'environnement eqnarray*, avec une étoile ajoutée à la fin du nom de l'environnement, donc.
Si vous êtes pinailleur sur la qualité de rendu des équations, vous aurez remarqué que eqnarray a inséré des espaces particulièrement grandes autour des signes =. Pour éviter ce phénomène gênant, il est recommandé d'utiliser l'environnement align fourni par le paquet de commandes amsmath. Placez donc
| \usepackage{amsmath} |
en préambule, et remplacez le code précédent par :
| \begin{align} 2\left(\frac{x}{y}\right) &= 8,\\ \frac{x}{y} &= \frac {8}{2}\\ &= 4. \end{align} |
Le résultat est maintenant nettement meilleur :
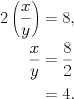
Notez qu'une seule esperluette par équation a été nécessaire à l'environnement align au lieu de deux pour eqnarray. Les équations sont également numérotées, et bien sûr, on peut faire référence à chaque équation, de la même manière que précédemment. Il existe là aussi un environnement étoilé, align*, qui supprime la numérotation.
Il vous faudra choisir entre l'environnement eqnarray et l'environnement align du package amsmath, car une fois ce dernier chargé, eqnarray risque de fonctionner de travers.
Pour ma part, le choix est fait depuis longtemps, car le paquet amsmath fournit également quantité d'autres environnements et commandes, qui deviennent vite indispensables à tout scientifique rédigeant des articles à fort contenu mathématique. Si vous êtes concernés, voyez sa documentation (par exemple ici, en anglais), pour avoir une idée de ses possibilités.
Du texte dans les équations
Une autre commande très utile fournie par le paquet amsmath est \text. Elle permet d'insérer du texte à l'intérieur même d'une équation, tout en conservant la police et le style du texte utilisés hors l'équation. En fait, elle permet au texte qu'elle prend en argument d'être composé en mode texte et non en mode mathématique. Ainsi, voyez par vous-même la différence entre :
| \[ E_{pot} = mgh \] |
et
| \[ E_\text{pot} = mgh \] |
Si l'on souhaite un style particulier pour ce texte, qui ne soit pas celui environnant l'équation, vous pouvez utiliser soit une des commandes de changement de style déjà vues, du genre
| \textbf{texte} |
soit utiliser les commandes analogues spécialement prévues par LaTeX pour le mode mathématique. Il y en a une pour chaque style (sauf les styles « incliné » et « petites capitales ») :
| Italique | \mathit{texte} |
| Gras | \mathbf{texte} |
| Machine à écrire | \mathtt{texte} |
| Sans serif | \mathsf{texte} |
| Roman | \mathrm{texte} |
Mais attention, contrairement à \text, le texte en argument de ces dernières commandes est composé en mode mathématique. En particulier, on l'a vu, les espaces entrés au clavier seront purement et simplement ignorés.
De plus, les caractères accentués ne doivent pas être entrés directement dans une formule mathématique (sous peine d'engendrer une floppée de « Warnings » dans la console). Les accents font l'objet de commandes spéciales en mode mathématique, et ces commandes sont différentes même de celles qu'on utilisait « dans l'ancien temps » pour le mode texte (cf. partie 2.). Par exemple, pour obtenir un « e accent aigu », on devra entrer \acute{e} pour l'accent aigu sur le e, au lieu de \'e. Ce qui devient vite très, très lourd à gérer.
Il est donc conseillé de réserver l'emploi des commandes \math… aux symboles et aux variables mathématiques qu'on voudrait dans un style donné, et d'utiliser les commandes \text… pour les véritables portions de texte.
Par exemple, sachant que les conventions mathématiques exigent souvent qu'un vecteur soit noté en gras, pour obtenir la propriété sur les vecteurs suivante :
![]()
j'ai entré ceci :
| a \mathbf{x} = \mathbf{0} \qquad \text{équivaut à} \qquad a = 0 \quad \text{ou} \quad \mathbf{x} = \mathbf{0} |
Les fonctions usuelles
Par convention, en mathématiques, les noms des fonctions usuelles (log, tan, sin, etc.) doivent être transcrits en caractères droits, contrairement aux symboles et variables qui, on l'a vu, doivent être en italique. Pour écrire les noms de ces fonctions, on dispose donc de commandes particulières, plus rapides d'emploi qu'en passant par \text ou \mathrm :
| tangente | \tan |
| cosinus | \cos |
| sinus | \sin |
| log népérien | \ln |
| logarithme | \log |
et j'en passe (fonctions hyperboliques, fonctions trigonométriques inverses, etc.)
Matrices
Pour écrire une matrice (et donc un vecteur), on utilise l'environnement array. Il fonctionne exactement comme l'environnement tabular vu à la leçon précédente, à cette différence près qu'il ne fonctionne qu'en mode mathématique. Par exemple, le code
| \[ A=\left(\begin{array}{ccc} 1 & 2 & 3\\ 4 & 5 & 6\\ 7 & 8 & 9 \end{array}\right) \] |
donnera
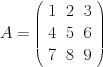
Vous pouvez évidemment placer n'importe quel élément dans cette matrice, que ce soit un chiffre, une équation ou une autre matrice !
Le paquet amsmath fournit quelques autres environnements spéciaux pour créer des matrices, plus simples à coder, mais un peu moins souples. Voyez, là aussi, sa documentation.
Les palettes de TeXShop
Il est commun en mathématique d'utiliser des lettres grecques pour désigner certaines variables du problème. Avec LaTeX, il vous suffit de connaître votre alphabet grec (vous en connaissez déjà deux lettres : « alpha » et « beta » qui ont donné leur nom à l'alphabet). En effet, il vous suffit d'entrer une contre-oblique suivi du nom de la lettre. Si vous mettez une majuscule au nom de la lettre grecque, vous obtiendrez sa version majuscule, si vous mettez une minuscule vous obtiendrez sa version minuscule. Par exemple,
| \[ 2\pi + \Omega = \xi \cos(\theta+\phi) \] |
donnera
N'oubliez pas que les commandes donnant les lettres grecques, comme quasi toutes celles présentées dans cette section, ne fonctionnent qu'en mode mathématique. Par conséquent, même si vous souhaitez obtenir ces lettres en dehors d'une formule proprement dites, encadrez-les par deux symboles $, comme ci-dessous :
| Les lettres $\alpha$ et $\beta$ sont très employées en mathématiques. |
Si vous ne le faites pas, LaTeX ne reconnaîtra tout simplement pas ces commandes et les signalera comme des erreurs.
Mais comme on n'attend pas de vous que vous sachiez votre alphabet grec sur le bout des doigts, TeXShop met à votre disposition la « Palette LaTeX ». Vous la trouverez dans le menu « Fenêtres » ou avec le raccourci « pomme-= » :
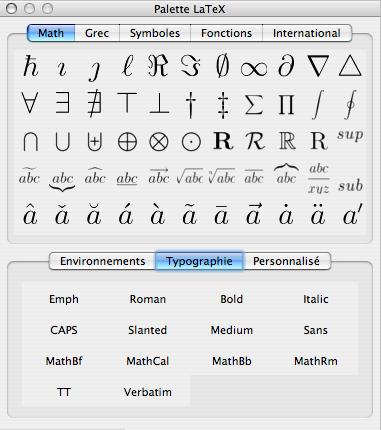
Dans la partie supérieure de cette palette, vous trouvez cinq onglets destinés aux mathématiques, avec tout d'abord les symboles spéciaux (constante de Planck, opérateurs d'ensembles, l'ensemble des nombres réels, etc.), puis les lettres grecques, puis quelques symboles (opérateurs logiques, parenthèses, etc.), puis les fonctions trigonométriques dont je vous parlais à l'instant. Le dernier onglet est peu important puisqu'il vous permet d'écrire les accents « à l'ancienne ».
Bizarrement, TeXShop oublie de mentionner dans cette palette que les commandes donnant certains symboles importants (par exemple \mathbb{R} qui donne l'ensemble des nombres réels) ne sont définies que si on charge un nouveau paquet : amssymb. Comme pour amsmath, je vous conseille donc de le charger systématiquement en préambule de votre document :
| \usepackage{amsmath, amssymb} |
La partie inférieure de notre « Palette LaTeX » possède trois onglets. Le premier reprend les environnements les plus courants (center, figure, table, tabular, itemize, etc.). Le deuxième vous donne les différents styles de texte, en mode texte et en mode mathématique. Enfin, le dernier onglet est une aide à la structure du document, dans lequel vous retrouvez les sections, le titre, etc.
Il existe également une deuxième palette, la palette « Matrix » (rien à voir avec le film) :
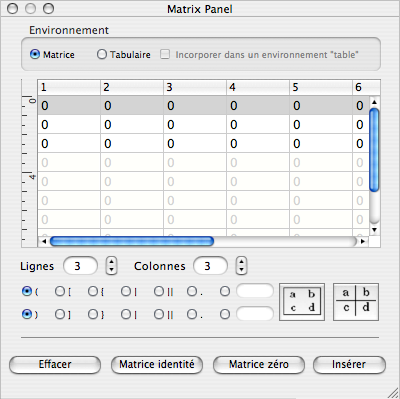
Cette palette est une aide à la création de matrices. Vous pouvez y définir la taille de la matrice, son contenu, ainsi que les contenants (parenthèses, crochets, norme, etc.)
Ces palettes sont donc une alternative ou un complément aux macros. C'est selon votre goût personnel. Pour ma part, comme je l'ai mentionné plus haut, je fais tout au clavier, les environnements que j'utilise le plus ont donc tous un raccourci-clavier.
Bien entendu, je pourrais encore écrire des kilomètres à propos des équations, tant les possibilités sont immenses. Mais je préfère vous donner un petit aperçu et lors de la dernière partie (la prochaine !) je vous donnerai une série de liens vers des documents de référence qui vous aideront à approfondir le sujet.
Je n'irai donc pas plus loin avec les mathématiques et je vous donne rendez-vous pour la prochaine et dernière partie de notre découverte de LaTeX.
Fabien Conus

, le 22.09.2008 à 09:55
Tu as fais la petite erreur du lien admin au lieu du lien réel : http://www.cuk.ch/articles/2092
Quand tu veux faire un lien sur un précédent article et que tu es connecté en admin, il faut copier/coller le lien dans la case “Lien public:” et non celui de ton champs d’adresse du navigateur ;)
, le 22.09.2008 à 10:07
Je suis d’accord avec Franck, l’écriture des équations en mode texte est imbattable. Toutes les solutions graphiques assistées ne sont pas efficaces.
Maintenant, il est clair que beaucoup veulent des formules mathématiques jolies dans une présentation Keynote par exemple, sans devenir fou à faire des slides dans Latex (oui, oui, je sais Franck, c’est super simple de faire des slides en Latex).
La solution : LatexIt
LatexIt permet d’utiliser la puissance de l’éditeur d’équation de Latex sans ses contraintes :)
Pas beau, la vie?
, le 22.09.2008 à 10:25
Pour l’erreur du lien, c’est corrigé !
Et ça ne rend pas fou, j’en suis la preuve vivante. (c’est moi ou j’entends des rires étouffés derrière moi ?)
Sérieusement, avec Beamer ça se rapproche même du jeu d’enfant. Je fais toutes mes présentations avec cette classe ! J’ai un article en projet sur elle, d’ailleurs. Si mon planning est respecté, ce serait pour novembre.
, le 22.09.2008 à 11:06
Oui, c’est mieux de ne pas faire des liens vers l’admin!:-) Même si ça m’arrive aussi, vu que c’est ce qui semble a priori le plus logique.
Merci pour ce nouvel article. Je regarde, je contemple, et je me dis que ce n’est toujours pas pour moi!
Vive le wysiwyg!!!
J’ai dit.
, le 22.09.2008 à 11:47
Commentaire d’ordre général :
J’ai commencé à écrire des articles scientifiques il y a deux, trois ans en LateX sous l’impulsion de Franck et de son directeur de thèse qui ne comprenaient pas comment je pouvais supporter de faire ça avec Word et consorts…
J’ai pourtant commencé avec Jane sur Apple II, puis MacWrite sur Mac, puis Word 5, puis Office up to 2004, et mon capital inertiel était diablement fort.
Eh bien ! je dois dire aujourd’hui que je ne comprends comment je ne m’y suis pas mis avant. Alors, ce que je suggère, c’est que ceux qui n’ont pas essayé se disent qu’ils devraient le faire avant de conclure…
C’est vrai qu’il faut un effort initial, mais comme pour toute utilisation de jobs pour lesquels on doit lire la doc avant d’aller taper aux portes d’autrui.
Et, pour illustration, je viens d’envoyer les cours de Franck à mon dernier thésard qui réside à Tunis, marre que j’en avais de reprendre ses Worderies pour les passer en LateX…
Merci, Franck !
J’ai dit, Joseph Pastor.
, le 22.09.2008 à 11:49
Comme je me sens d’humeur provocatrice aujourd’hui, je conseille la lecture de cet excellent article sur les traitements de texte wysiwyg :-)
Edit : faudra qu’on m’explique comment l’intervention de Joseph (salut papa, au fait ;-)), qui est inscrit sur cuk.ch, a pu être mise sous mon nom alors qu’on est 700 km l’un de l’autre en ce moment !
Edit bis :
De rien ;-) Mais il faut aussi remercier Fabien, c’est lui qui est à la base de tout ça ! Et François, qui même opposé personnellement à LaTeX, permet la parution de cette série.
, le 22.09.2008 à 14:40
Mais je ne suis opposé à rien du tout!:-)
Moi tant que ça plaît ce Latex, ça plaît, et c’est tant mieux.
Chacun ses goûts. Je n’aime pas les balises, et je n’ai pas d’écrits scientifiques à produire, alors voilà… Cela dit, j’en aurais, que je l’utiliserais sûrement, ce Latex.
Noé par exemple est totalement convaincu!
, le 22.09.2008 à 15:28
En fait, Noé s’est converti récemment à ConTeXt, un concurrent de LaTeX basé sur le même programme (TeX). Ceci dit, ConTeXt n’est pas plus wysiwyg que LaTeX ;-)
Et pour l’intervention de Joseph à mon nom, c’est juste qu’il y a quelques semaines je m’étais connecté à cuk.ch sur son ordi, et que j’ai oublié de me déconnecter avant de quitter le site. Résultat, cookies aidant, Joseph s’est retrouvé à rédiger sous mon nom sans le savoir.
, le 22.09.2008 à 15:34
Surtout les balises en cartòn!
Milsabor!
, le 22.09.2008 à 16:51
Bah, là du coup, sérieusement, j’ai du mal à garder mon sérieux :p
, le 22.09.2008 à 17:27
C’est toujours la même histoire avec LaTeX, Guillôme, et c’est vrai au carré avec Beamer : si tu te contentes des styles de présentation offerts par défaut, c’est vraiment facile (oui, d’accord, il faut être débrouillé avec LaTeX, quand même !), et j’espère le démontrer dans mon futur article. Mais si tu souhaites personnaliser, tu vas droit dans les problèmes…
Ça va mieux, dit comme ça ? :b
Et au juste, je lis l’article que tu viens d’achever dans la zone admin, je lui trouve un soupçon de mauvaise foi lors d’un certain passage ;-)
, le 23.09.2008 à 05:07
Je suis avec beaucoup d’intérêt cette série d’articles sur Latex.
Étant complètement débutant dans Latex (j’utilise MathType 6), pouvez-vous m’indiquer le ou les Logiciels indispensables, au début, pour maitriser rapidement (et sans trop souffrir !) Latex et en particulier pour les Maths.
Plusieurs noms de logiciels étaient cités dans le 1er article, mais aucun, il me semble, “ne ressortait ” nettement.
Merci pour vos réponses.
, le 23.09.2008 à 08:41
Delos, tu parles des éditeurs de texte dédiés à LaTeX ? Ou des manuels sur LaTeX ? À mon avis, choisir le bon manuel d’introduction à LaTeX est plus important que le choix de l’éditeur. Tu arriveras toujours à faire du LaTeX quel que soit l’éditeur, il faut juste que tu trouves celui qui est le plus « convivial » à ton goût.
Question manuel, un bon choix est… ce cours ;-) et après, ce manuel en français (la première partie), ou celui-là en anglais.
Si tu parles d’un éditeur dédié, je n’en ai utilisé que deux sur Mac : TeXShop et Texmaker. Texmaker a quelques atouts pour le complet débutant, à mon avis. Il dispose notamment d’un manuel de référence LaTeX dans son aide, qui est sûrement très pratique. Mais il est très limité par le fait qu’il ne dispose pas d’un lecteur de PDF incorporé. Donc TeXShop (celui choisi pour ce cours-ci) me paraît un meilleur choix dès le moyen terme. De plus, TeXShop propose dans son aide quelques aides pour commencer LaTeX, en anglais.